Biomechanics: Efficient Runner Model Rev 1.1

Mathematical Analysis utilizing biomechanics and basic physics can be used to determine the energy cost of various running factors. When the energy cost is known and compared to empirical data the time penalty associated with these factors can be determined. Running variables, combinations thereof, and their effect on performance that can be readily analyzed include:

Shoe weight
Shoe cushion & heel to forefoot differential
Over-stride/cadence
Excess body weight
Foot strike

This post establishes the basic model that will be used for the separate analysis of each of these factors. Assumptions and initial conditions are also defined. This is a crude model intended to capture the gross movements, which account for the majority of energy cost.  This update from Rev 1.0 modifies the figure to clarify center of mass position relative to foot strike and adds the parameters and calculations used to determine the energy cost of striding and vertical displacement.

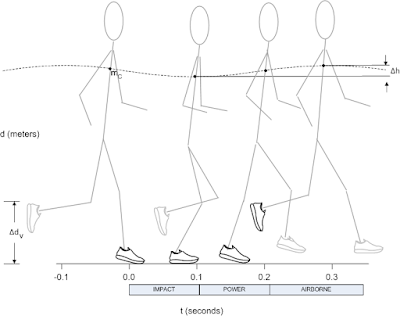
A visual examination of efficient runners was necessary to create a proper model. An optimal stride was found to be one that places the center of mass directly over a slightly bent knee when the foot strikes. Cadence is equal to or greater than 180 foot strikes per minute and a forefoot strike is employed.  Both low cadence (over stride), and the use of a heel strike reduce efficiency.¹  

The two gross movements which constitute the majority of energy expenditure are striding and vertical displacement.

Striding
For each stride the foot is accelerated up and forward requiring energy. The energy cost of striding can be calculated using Newton’s laws of motion and by treating the legs and shoes as point masses. For these calculations the leg was divided into separate masses consisting of the shoe, foot, calf, and thigh. Examination of a stride reveals the respective distance each point mass travels with respect to the hips.

The mass contributions m were found in percent total body weight with respect to one limb.  The horizontal distance  ∆d_h  traveled was found as a percentage of stride length L.  The vertical distance ∆d_v traveled is a percentage of total body height. ²

 

	m [%]	∆dh [%]	∆dv [%]
Thigh	6.7	15.4	-
Calf	2	46	-
Foot	2	100	26.7
Shoe	-	100	26.7

When the pace and cadence are known the stride length L and acceleration a of each point mass can be readily determined.

L = 1/(pace•cadence)
a =  2∆d/t²

When acceleration is known the force F required to accelerate each point mass can be found.  Energy E is then calculated for each point mass, summed, and converted to food Calories.

F = ma
E = F∆d

As the total striding energy is calculated per stride it must be multiplied by cadence and optionally pace to place it in terms of either time or distance respectively.  Dividing by 4184 will convert Joules to food calories.  When analyzing striding, the power generated to push off the ground is ignored, as it is captured by the center of mass and conversion of energy calculations.

Center of Mass and Conservation of Energy:

The energy cost related to center of mass displacement can be calculated using a spring mass model and Hooke’s law.  The center of mass m_C follows the dashed sinusoidal path of amplitude ∆h.  When cadence is known ∆h can be readily calculated using equations of motion. 

∆h = ½(9.8)(t_STRIDE/2)²

The vertical component of the Kinetic energy of the runner can be calculated when the height is known.  This is the energy of each foot strike E_K.

E_K = (m_C)(9.8)( ∆h) 

Additionally the shoe, foot, leg, and torso can all be modeled as one equivalent spring or separate springs in series.  Here the leg is treated as one equivalent spring.

Central to calculating center of mass energy costs is the conservation of energy.  Each stride transfers some energy to the next, loses energy to the environment, and adds additional energy from muscle contractions.  To find the energy the leg captures E_LEG the spring constant of the leg must be known or the force exerted on the spring at its maximum compression must be known.  From the work of Lieberman the force is known to be 2.5 body weight.

E_LEG = ½ (F)(m_C)(9.8)(½∆h)    

To maintain a steady pace the energy lost to the environment is equal to the propulsive energy of muscle contractions.  The energy expended to maintain vertical movement E_V is thusly:

E_V = E_K - E_LEG

Once again, as the vertical energy is calculated per stride it must be multiplied by cadence and optionally pace to place it in terms of either time or distance respectively .  Dividing by 4184 will convert Joules to food calories.  The total energy cost of running is the sum of the striding and center of mass calculations.

*

¹ The gross movements for a heel strike and forefoot strike were found to be the same, notable differences exist in the impact forces.  The stride time t_STRIDE can be calculated by  dividing 60 seconds by cadence.

² Mass and height contributions are for a 5’8” 145lb 10.7% body fat male.

*

Please feel free to refute any part of this post or add detail that has been missed.  While my intent is to fully explain things I do not always succeed and some nuances have been omitted in the interest of brevity.  I am happy to discuss in further detail as required.